On security

Your ad here if you win

Even though Ergon changes only the supply design, the consequences are massive. Not only for the stability and fairness of the system but also in other areas. In this post, I want to argue the change improves the security of the Nakamoto Consensus.
The article assumes the knowledge of how Bitcoin consensus works.
In the case of proportional reward, the value of the reward is adjusted with the number of coins instead of the currency value. The security budget works the same way as in Bitcoin but instead of being dependent on the price per unit it is being adjusted by the number of units. Ultimately, the security budget always boils down to the demand for new coins (neglecting the fees). If there is oversupply, in the fixed reward system the price will keep dropping as the supply is getting diluted with the unrequested coins. Alternatively, in the proportional reward system the block reward size will keep dropping, while preserving the unit value. We can prove that by returning to the equations from the ergon whitepaper.
With a small modification, we can fully solve the Bitcoin model for both price and hashrate. Compared to the solution from the white paper, we are replacing the demand expressed in the coin units with demand expressed in the external currency units - for instance dollars. Instead of considering demand of e.g. 10 coins per day, we will consider demands like $10,000 per day.
The equations for Bitcoin model are as follows:
The impulse response of the price is while the impulse response of the hashrate is . This means we could feed the demand data by making convolution between the demand function and price's impulse response, then feed that price to the hashrate's impulse response. We can see that price is inversely proportional to the reward, while hashrate is directly proportional to the demand. It means that hashrate is directly proportional to the demand, and where it settles doesn't depend on the reward. Additionally, when doing the convolution in the hashrate, the exponent is integrated and the final result is proportional to the demand (in dollars) divided by - the cost of electricity. This result agrees with numerical solutions, which you can see here (pdf). If you are familiar with SageMath, you can play around with this notebook and check different demand scenarios - how the hashrate adjusts to demand in both cases.
The Ergon nodes follow the most accumulated Proof of Work chain. The miners doing the work receive the reward for the blocks they solve. With new blocks being built on top of previous blocks, older transactions are accumulating the work done on top of them. Any miner can add a transaction to the ledger and confirm it. This is what makes transacting unstoppable. To reverse a transaction, a miner has to redo the proof of work up until that transaction and outpace the honest miners. With less than 50% of the network computational power, it quickly becomes impossible. A miner with more than 50% of the hashpower is able to:
In the scenario of a longer attack like a censorship attempt, such that the difficulty manages to adjust, fixed reward and proportional reward systems have different properties in favor of the proportional reward. The following consideration is not relevant to short bursts, where fixed reward acts as if it were proportional, due to the expected block time also being affected by additional hashrate.
Consider the following scenario for the fixed reward:
If only every second block gets orpnaned, the attacker and other potential participants are still getting rewarded for that on average.
The proportional reward changes this picture. When the DAA kicks in, it reduces the reward as well. In the scenario above, the attacker would be receiving roughly half of the reward every block and exactly the same reward per day, because:
Hence, the reward rate is proportional only to the hashrate. Halving the time halves the rewards. Doubling the time doubles the reward. The reward rate is conserved.
The attacker receives the amount determined by his hashrate alone. There is no orphaning bonus.
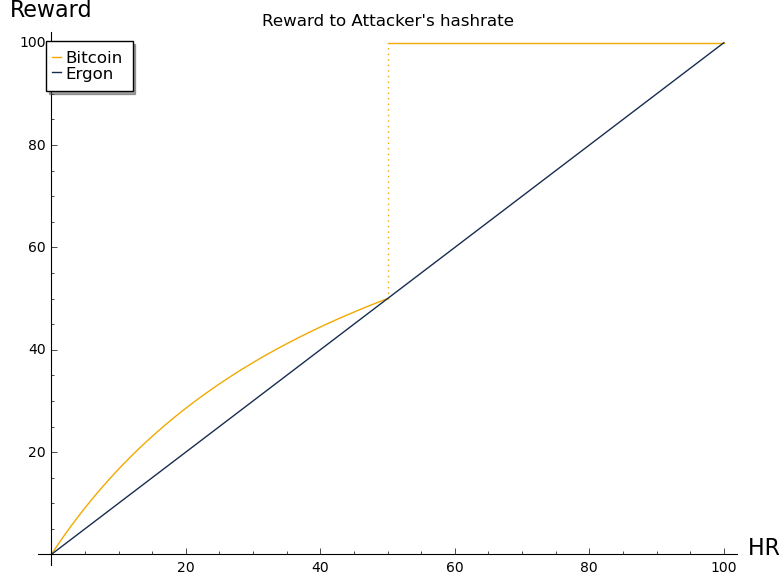
The attacker not only undermines the validity of his own wealth when performing the attack, he also receives less reward compared to Bitcoin while doing so, The intrinsic incentives against the scenario of a chain take over, censorship and very deep reorgs are more favorable with the proportional reward system.
The incentives of a miner are described by Satoshi Nakamoto in the whitepaper:
The incentive may help encourage nodes to stay honest. If a greedy attacker is able to assemble more CPU power than all the honest nodes, he would have to choose between using it to defraud people by stealing back his payments, or using it to generate new coins. He ought to find it more profitable to play by the rules, such rules that favour him with more new coins than everyone else combined, than to undermine the system and the validity of his own wealth
This is a general consideration applicable to both systems. The miner that is capable of performing a 51% attack to double-spend his payments can either reorg the block that he have already mined or reorg someone else's block. If he reorgs his own block, he loses the reward. If he reorgs someone else's block, he doesn't actually lose anything, both in Bitcoin and Ergon he is rewarded a normal reward. He can steal his spent coins back, but at the cost of making an earthquake crisis for the chain, potential loss of the market and liquidity and not being able to liquidate his coins. If he doesn't value those coins enough to want the chain healthy and adopted, why would he want them back? Let us put some numbers on it.
Follow this recipe to perform the attack:
Summary: You're left with X dollars that we had to begin with, X worth of coins plus mining rewards, minus whatever you spent on mining. You have started with X dollars to buy the coins, so they don't count. The following equation has to be fulfilled for the operation to break even:
,
where is a value retention factor and r is the reward assuming the cost is equal to the reward - neglecting the miner's margin, which is usually thin.
The blockchain then secures up to the following transaction size on each confirmation:
If the attacker is able to sell the coins for 1/10th of their initial price, the retention factor is 0.1 (which is probably quite generous), the chain effectively secures transactions of the value 9x higher than the reward in one confirmation. Two confirmations secure 18x the reward size and so on.
This result gives us a tangible, though parametric description of how many confirmations one should wait to consider a transaction final, given the value of the transaction.
For example, one Bitcoin confirmation secures around $2.7 million sized transactions with 6.25BTC block reward and $48,000 price and 0.1 value retention factor. Compared to the market cap, it's 0.00028% of the market capitalization. Comparatively, at the time of writing this article Ergon has an order of magnitude higher proportion of security to the market cap than Bitcoin, while we are at the bottom of an impulse response huge oscillation.
This comparison is meaningful with regard to how many coins do people have on them to begin with. How available are the amounts that would justify the attack on the network and how big of an impact can a one-off attack get, once the profitability can be reached. In the bird's-eye view, the total supply of Ergon is equal to chain's accumulated proof of work modulo Moore's law correction. Because of that, the ratio of the budget to the market cap is very likely to stay high. Ergon supply doesn't grow without massive resource investments. The market capitalization is not "hacked" by the deep capital that is waiting to exit.
In parallel to the availability goes fair distribution - concentration of coins from pre-mine or early mining that happens with the Bitcoin supply model favors the select few early adopters or founders with immense power over the network, including the ability to perform larger attacks. Ergon have always been equally hard to mine, allowing the participants joining at different times to play by the same rules and preventing the existence of deep capital, that is uniquely positioned to attack the network. An attacker would have to acquire the coins somehow, likely summoning more hashrate as an unintended consequence and making the attack more difficult for himself.
After a shock, the proportional reward systems' hashrate oscillates around an equilibrium before it stabilizes at the level reflecting the current demand for new coins. This is potentially an issue during the large shifts in the environment. Hopefully, it's a problem of infancy. The shocks have lower impact as the liquidity grows, and it becomes less likely an instantaneous demand will be a great portion of the market capitalization or exceeds it. The lack of dynamic arbitrage principle states that no such thing as predictable oscillations should be happening on a liquid market, therefore the fact that they do appear follows from lack of thereof.
Any double-spending attack on an exchange can only steal what is in the order books, but also if the order books are broad, the system becomes less prone to the oscillations. So when the oscillations are severe it means there is not much to steal and when there is much to steal, there are no more oscillations. Those factors are negatively correlated in just the right way.
Under the normal conditions, the hashrate depends on the demand for new coins, both in Bitcoin and in Ergon. Ergon's proportional reward affects the Nnakamoto Consensus positively in the scenario of a long-lasting attack attempt, and the fair distribution resulting from the proportional reward removes the parties best positioned to attack the network. The issue of hashrate oscillations is hopefully a temporary growing pain. Overall, proportional reward has the potential to be more censorship resistant and in practice more secure than Bitcoin.